❮ Go Back

Syntax Reading and Exercises for Exam 2

Instructions

Exercises C (Grammars, Parse Trees)

Read sections 2.3 (Lexical Syntax) and 2.4 (Context-Free Grammars) on pp. 33 – 41 of Sethi Do problems 2.4, 2.6, 2.9, and 2.14 on pp. 49 – 51.

Problem 2.4

Give context-free grammars describing the syntax of each of the following:

Problem 2.6

For each of the following strings, draw a parse tree with respect to the grammar for arithmetic expressions in Fig. 2.6:

Note: E stands for Expression, T for Term, F for Factor

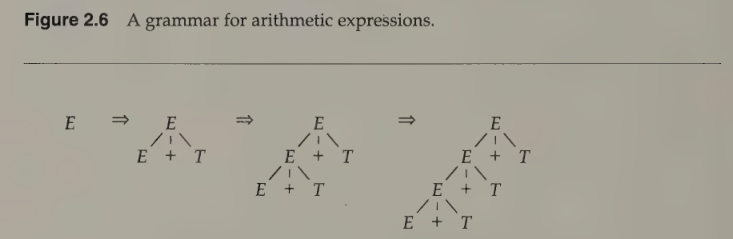
alt text

Problem 2.9

The BNF rules in each of the following cases describe a construct that consists of a list of elements. Describe the list. How many elements does it have? Does anything appear between or after the elements?

Problem 2.14

The following grammar is based on the syntax of statements in Pascal:

S  ::= id := expr
    |  if expr then S
    |  if expr then S else S
    |  while expr do S
    |  begin SL end

SL ::= S
    |  S ; SL

Note: There is a misprint in the original problem. The first production with SL on the left should read "SL ::= S" rather than "SL ::= S ;".

Draw parse trees for each of the following:

Exercises D (EBNF)

Read the Extended BNF subsection of Sec. 2.6. Do problems 2.9 and 2.16a†† on pp. 50 – 52.

†† Re 2.16: The first line of the EBNF specification on p. 52 uses [ ] to mean an empty string.

Problem 2.16(a)

The following EBNF grammar is based on the syntax of statements in the Modula-2 programming language:

S  ::= [ ]
    |  id := expr
    |  if expr then SL { elsif expr then SL } [ else SL ] end
    |  loop SL end
    |  while expr do SL end

SL ::= S { ; S }

Token id represents a variable and token expr represents an expression. Note that [ ] stands for the empty string.

Exercises E (Derivations, Grammars for Expressions, Syntactic Ambiguity, Syntax Charts)

Do problems 2.5¶, 2.6, 2.10‡, 2.11, 2.12§, 2.13§, 2.15a, 2.15b, and 2.16b on pp. 49 – 52.

¶ Re 2.5(a): A leftmost derivation is a derivation in which the leftmost nonterminal is replaced at each step. A rightmost derivation is a derivation in which the rightmost nonterminal is replaced at each step. The derivation of 2 1 . 8 9 from real-number that is shown on p. 41 is a leftmost derivation:

alt text

For example, its second step replaces the leftmost nonterminal (integer-part) in the string integer-part . fraction with integer-part digit, and then its third step replaces the leftmost nonterminal in the string integer-part digit . fraction with digit. The second step of a rightmost derivation of 2 1 . 8 9 from real-number would replace the rightmost nonterminal (fraction) in the string integer-part . fraction with digit fraction

‡ Hint for 2.10(b): Put the unary – operator in the same precedence class as binary + and binary –

§ Even though problem 2.12 does not say this, the grammar you write for that problem must be able to generate expressions that involve ! (the logical negation operator) as well as the binary operators shown in Figure 2.9; otherwise you will not be able to do parts b and c of problem 2.13. ! is a right-associative unary prefix operator and has higher precedence than any binary operator.

Problem 2.5

Consider the grammar for real numbers in Fig. 2.3:

alt text

Problem 2.10

The operators of Pascal are as follows (the in keyword tests set membership):

<  <=  =  <>  >=  >  in
+  -  or
*  /  div  mod and
not

All of these operators are left associative. All operators on the same line have the same precedence. The lines are in order of increasing precedence.

Problem 2.11

For each of the following expressions, draw parse trees with respect to your grammar for Exercise 2.10.

Problem 2.12

Write an expression grammar using the table of C operators in Fig. 2.9.

alt text

Solution

It is clear from problem 2.13 that the ! operator should be included in the table; in C/C++ ! has higher precedence than all other operators in the table, and it is right-associative.

<class 1 prefix op> ::= !
<class 2 binary op> ::= * | / | %
<class 3 binary op> ::= + | -
<class 4 binary op> ::= << | >>
<class 5 binary op> ::= < | > | <= | >=
<class 6 binary op> ::= == | !=
<class 7 binary op> ::= &
<class 8 binary op> ::= ^
<class 9 binary op> ::= |
<class 10 binary op> ::= &&
<class 11 binary op> ::= ||
<class 12 binary op> ::= =

<exp[0]> ::= <variable> | <constant> | ( <exp[12]> )
<exp[1]> ::= <exp[0]> | <class 1 prefix op> <exp[1]>
For 2 <= i <= 11,
  <exp[i]> ::= <exp[i-1]> | <exp[i]> <class i binary op> <exp[i-1]>
<exp[12]> ::= <exp[11]> | <exp[11]> <class 12 binary op> <exp[12]>

<exp[12]> is the starting nonterminal.

Problem 2.13

For each of the following expressions, draw parse trees with respect to your grammar for Exercise 2.12.

Problem 2.15

The following grammar is motivated by declarations in C:

   Declaration ::= Type Declarator ;
          Type ::= int
                 | char
    Declarator ::= * Declarator
                 | Declarator '[' number ']'
                 | Declarator '(' Type ')'
                 | '(' Declarator ')'
                 | name

Problem 2.16(b)

The following EBNF grammar is based on the syntax of statements in the Modula-2 programming language:

S  ::= [ ]
    |  id := expr
    |  if expr then SL { elsif expr then SL } [ else SL ] end
    |  loop SL end
    |  while expr do SL end

SL ::= S { ; S }

Token id represents a variable and token expr represents an expression. Note that [ ] stands for the empty string.